 |
 |
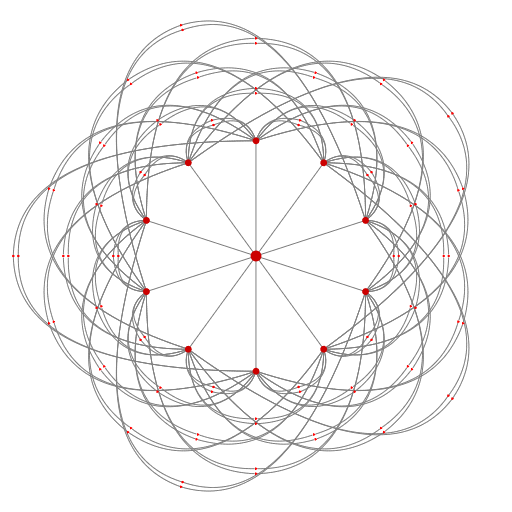
| Figure 1 | Figure 2a |
 |
 |
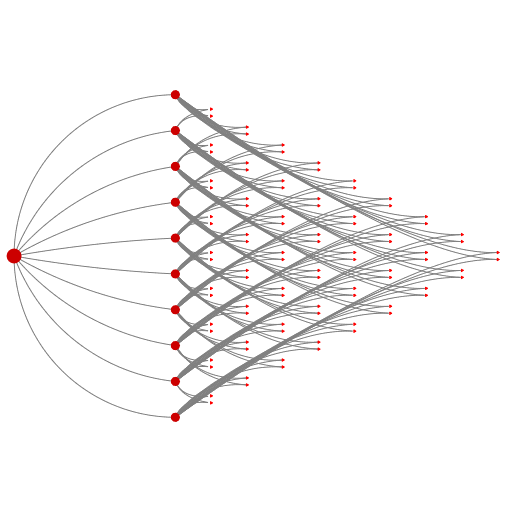
| Figure 2b | Figure 3 |
Contest Category: "Theoretical Graph Competition" (information)
Author: Michael J. McGuffin (Jurisica Lab, Ontario Cancer Institute and DGP Lab, Department of Computer Science, University of Toronto)
In this category, contestants are given a plain text description of "a 'mystery' graph of 101 nodes and 190 edges" and must design a visualization of the graph, either static or animated.
Result of contest: I tied for first place with another entry.
My solution:
After reading in the description of the graph in my home-grown graph browser and inspecting the structure, I designed three different depictions (one of which has two variations: see Figures 2a and 2b below) on paper. I noticed that the three depictions could be arranged in a progression that turns the layout of nodes inside-out, and so chose to implement an animation showing all the depictions (this turned out to be a bit more work than I expected!) The animation was implemented in C++ using OpenGL in my spare time over the course of a few days. Some of the arcs are drawn as quadratic Bézier curves, and some are drawn as circular arcs -- I wrote my own rendering routines for both of these. The motion paths followed by nodes and by control points are either straight line segments or are themselves circular arcs. The layouts in Figures 1 and 3 below are "turned inside out" with respect to each other, and Figures 2a and 2b show intermediate states.
Because this graph has a high degree of symmetry, it makes sense to use depictions that makes this symmetry obvious. Figures 1 and 3 show the subgraph that resembles a K10 clique using simple radial symmetry. Figures 2a and 2b use a less common arrangement, and are most interesting for the way they manage to fit all the arcs in the drawing without occluding nodes. One aspect I would have improved given more time is the layout of the 10 central nodes in Figure 3, which I tried to layout algorithmically in such a way as to make all the edge adjacencies obvious, but as can be seen this wasn't quite achieved for some of the nodes.
As a video:
(Note that when I play the videos on linux with mplayer, the aspect ratio is slightly off for some reason, and the video appears stretched.)
As a tiny executable for MS Windows:
Keyframes from the animation:
 |
 |
| Figure 1 | Figure 2a |
 |
 |
| Figure 2b | Figure 3 |