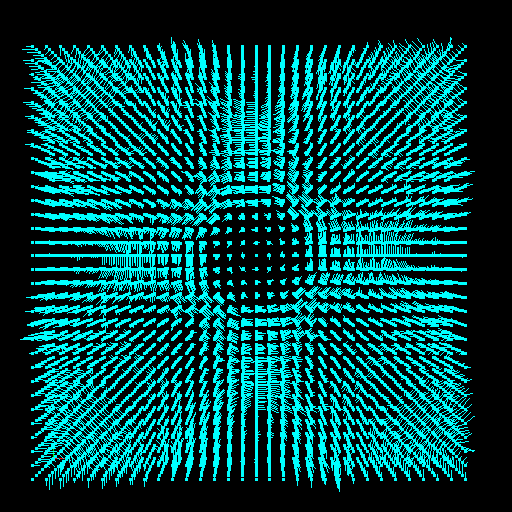
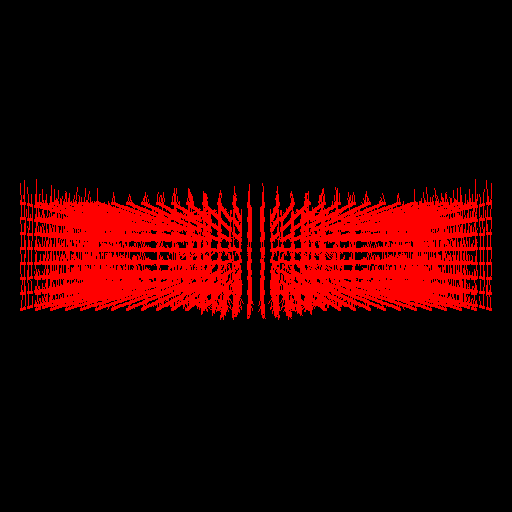
Below are screenshots of an interactive electromagnetic field simulator. This was implemented to begin exploring the challenges of visualizing two vector fields (the electric and magnetic components) over a 3D space. This is in contrast to the single velocity vector field that is of concern in fluid visualization.
The algorithm used for simulation is the Finite Difference Time Domain (FDTD) Yee algorithm, first published in 1966. Descriptions of the Yee algorithm are in
@book{taflove2000,
author={Allen Taflove and Susan C. Hagness},
title={Computational Electrodynamics:
The Finite-Difference Time-Domain Method},
year=2000,
edition={2nd},
publisher={Artech House}
}
In the implementation shown below, the grid wraps around, thus corresponding to one period of a periodic field. There are no boundaries or barriers in the simulation; the electric permittivity epsilon and magnetic permeability mu have constant values over the grid.
The mouse can be dragged to "paint" values into the magnetic field. The current implementation of this "painting" operation actually violates Gauss' law, however it's still interesting to visualize the reaction of the simulation interactively. Both simulations below show a field some number of time steps after an initial, single "brush stroke" that disturbed or "plucked" the magnetic field at the centre of the grid.


Above: snapshot of a simulation on a 32x32x8 cell grid. The first image shows an arrow plot of the electric field in cyan, seen looking along the z-axis. The second image shows an arrow plot of the associated magnetic field in red, seen looking down the y-axis.


Above: snapshot of a simulation on a 64x64x64 cell grid. The first image shows an arrow plot of the electric and magnetic fields in cyan and red, respectively. Unfortunately, the arrow plot is too dense to be informative. The second image shows, from the same point of view, sparsely sampled fluxlines of the electric and magnetic fields in blue and yellow, respectively. (Note that fluxlines in electric and magnetic fields are analogous to streamlines in a fluid.)
Acknowledgements
Thanks to Prof. Costas D. Sarris of University of Toronto,
and Liying Sun of Stanford University,
for guidance and advice in this topic.
Copyright ( C ) Michael McGuffin, 2004